Table of contents
1. Background
2. Receptive field
3. Convolution
4. CNN
4.1 Fully Connected Layer
4.2 Convolutional Layer
4.3 Output Size & padding
4.4 Pooling
1. Background
CNN이 나오게 된 배경
CNN(Convolutional Neural Networks)의 개념이 나오기 전까지 우리는 Multi-layered Neural Network(이하 MLP, Multi Layer Perceptron)를 사용했었다. 기존에 존재하던 MLP를 이용하여 이미지를 처리하기 위해서는, 이미지를 1차원 벡터로 쭉 펼쳐야 했다. 즉 MLP를 사용하기 전에 많은 전처리 과정이 필요했습니다.
하지만 이 지점에서 많은 문제들이 발생합니다.
공간적 정보(Spatial information)를 반영하지 못함

이미지는 공간적 정보를 가지고 있습니다. 예를 들면 다음과 같습니다.

- 공간적으로 가까운 픽셀들은 값이 비슷합니다.
- RGB, 3가지 채널 값들은 서로 밀접하게 연관되어 있습니다.
- 특정 픽셀과 거리가 먼 픽셀들은 서로 관련이 없습니다.
공간적 정보를 활용하지 못하면 Input 이미지의 픽셀이 조금만 달라져도 기존 MLP 네트워크는 새로운 클래스로 인식하고 처리합니다. 이미지를 1차원 벡터로 펼쳐놓았기 때문에 모든 이미지 입력값들이 위치와 상관없이 처리되기 때문입니다.

만약 손글씨로 쓰여진 5의 이미지가 여러 장 있을 경우, 필기의 모양이 다른 경우와 각도가 조금씩 다른(하나의 픽셀, 두 개의 픽셀이 다른 경우와 같이) 경우 모두 다른 정보로 인식한다는 것입니다. 즉 글자의 topology(위상학적)을 고려하지 못하고 pixel 단위의 raw data를 이용하기 때문에 좋은 결과를 기대하기가 어렵습니다. 따라서 좋은 결과를 기대하기가 어렵습니다.
이것이 기존 MLP의 한계점이고, CNN이 등장하게 된 배경입니다.
2. Receptive Field
David H. Huble과 Torsten Woesel은 1958, 1950년에 고양이의 시각 피질 구조에 대한 연구와 실험을 진행하였습니다. (시각 피질은 눈에서 오는 신호들을 처리하는 뇌의 한 부분입니다.) 이 실험의 contribution은 시각 피질 내의 많은 뉴런이 Local receptive field를 가진다는 것입니다. 이것이 의미하는 바는 하나의 뉴런은 모든 시야 영역에 대해 반응하는 것이 아니라, 특정 범위 안의 시야 영역에 대해 반응한다는 것이었습니다.

또한 실험의 결과를 정리하면 다음과 같습니다.
- 하나의 뉴런은 특정 시야 영역에만 반응하는 Receptive field를 가집니다.
- 하나의 뉴런의 Receptive field는 다른 뉴런의 Receptive field와 겹쳐질 수 있습니다.
- 이렇게 Receptive field들이 겹쳐져서 전체 시야에 반응하게 되는 것입니다.
그리고 각각의 뉴런은 저수준의 패턴을 인식하고 이것들이 모여 우리는 복잡한 패턴에 반응할 수 있다는 것을 알게 되었습니다. 즉 고수준의 뉴런들은 주변에 있는 저수준 뉴런의 출력에 기반하여 복잡한 패턴을 인식한다는 것을 알게 되었습니다.
첫 번째 아이디어인 Receptive field입니다.
Hierarchical organization
또한 시각 피질의 뉴런들은 계층 구조를 이루고 있습니다. 뉴런은 한 번에 모든 정보를 처리하지 않습니다. 저수준에서 고수준의 정보를 순차적으로 처리하게 되는데요.
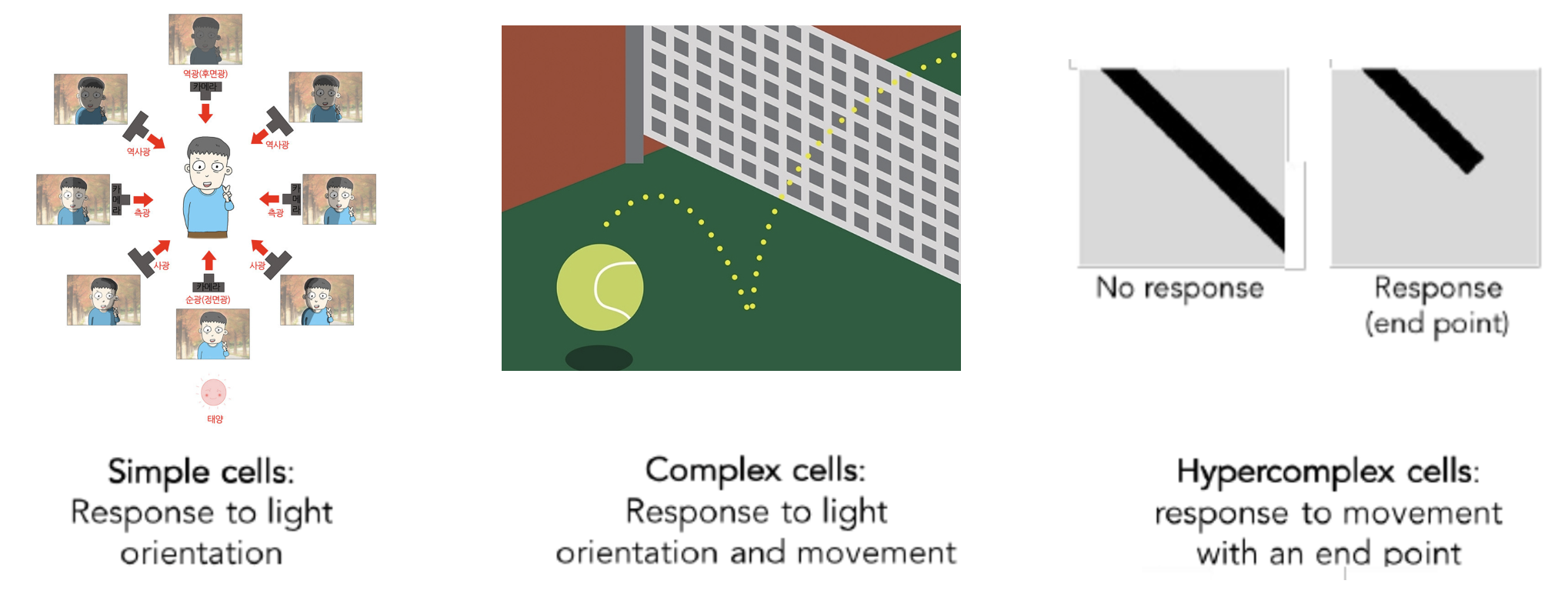
Simple cells
Response to light orientation
Complex cells
Response to light orientation and movement
Hypercomplex cells
Response to movement with an end point
(일대일로 번역하면 어색해져서 그냥 영어로 작성하였습니다. 영어로 읽고 이해해 보시면 더 잘 이해가 되실 겁니다.)
우선 simple cell에서는 빛이 들어오는 방향에 대한 정보를 인식합니다. 다음 계층인 complex cell에서는 물체의 움직임에 대한 정보를 인식하게 됩니다. 다음 계층인 Hypercomplex cell에서는 물체의 엣지(모퉁이.?)를 인식하게 됩니다. 이렇듯 간단한 패턴에서 복잡한 패턴을 순차적으로 인식하게 되는 구조를 가지는 것을 알 수 있습니다. 이러한 고양이의 시각 피질에 대한 실험의 결과에서 아이디어를 얻어 CNN이 만들어지게 되었습니다.
두 번째 아이디어인 계층 구조입니다.
3. Convolution
CNN은 위에서 본 첫 번째 아이디어와 두 번째 아이디어를 합쳐서 공간적 정보를 반영할 수 있게 되었습니다. CNN의 전체 아키텍처를 보기 전에 Convolution이라는 연산을 이해해야 합니다. Convolution이란 "합성곱 or 곱해서 더한다"라는 의미를 가집니다.
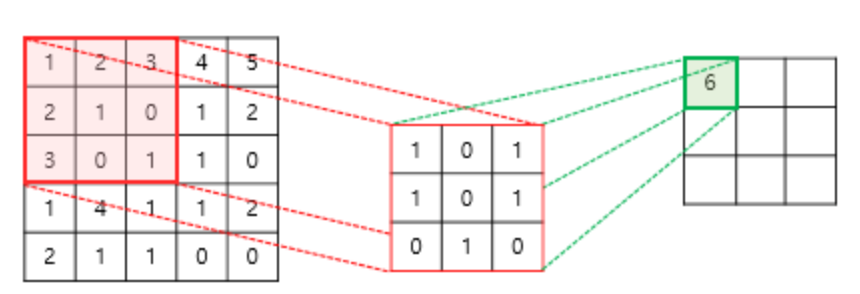
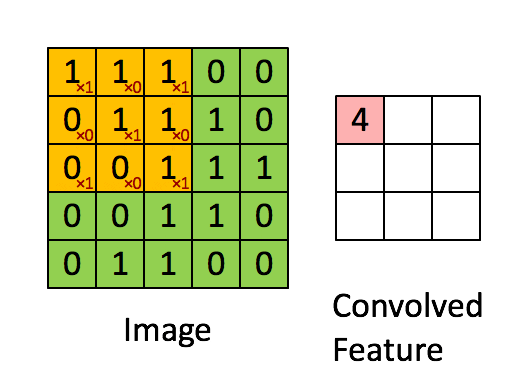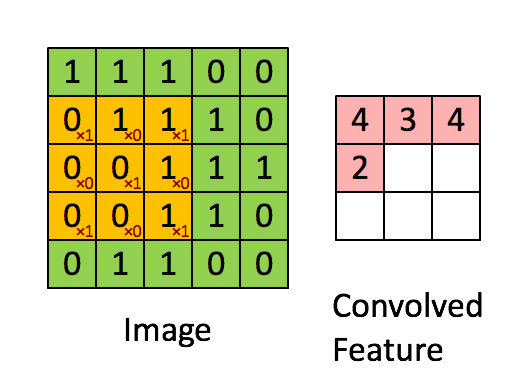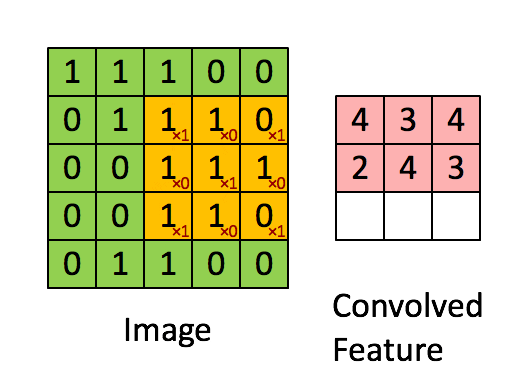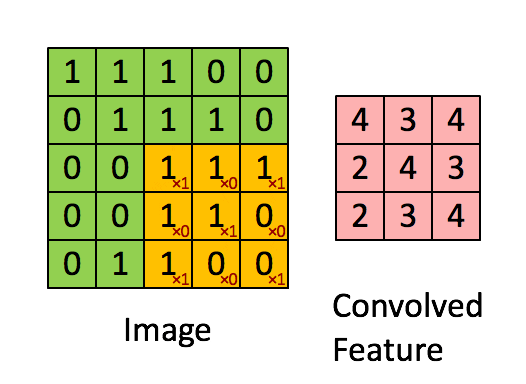
위 그림을 살펴보도록 하겠습니다. 세 가지 정사각형이 있는데요. 먼저 CNN이 입장에서 생각해 보겠습니다. 제일 왼쪽 정사각형은 input 이미지, 중간은 필터, 제일 오른쪽 정사각형은 output 이미지입니다. 이제 시각 피질의 입장에서 생각해보겠습니다. 제일 왼쪽 정사각형의 빨간색 부분이 시각 피질 뉴런의 Receptive field, 중앙의 정사각형이 뉴런, 오른쪽 정사각형은 우리가 이미지를 인식한 결과라고 할 수 있습니다. 이렇듯 CNN의 Architecture는 시각 피질의 Architecture를 완벽하게 모방한 네트워크라고 보시면 됩니다.
또한 위 그림을 통해서 합성곱의 진정한 의미를 이해할 수 있는데요. 위 그림에서 필터(중앙 정사각형)와 Receptive field(왼쪽 정사각형 빨간색 하이라이트 부분)를 element wise로 곱한 후 더하는 연산(최종 결과는 오른쪽 정사각형의 초록색)을 볼 수 있습니다. 이것이 바로 합성곱입니다. 매우 간단합니다.
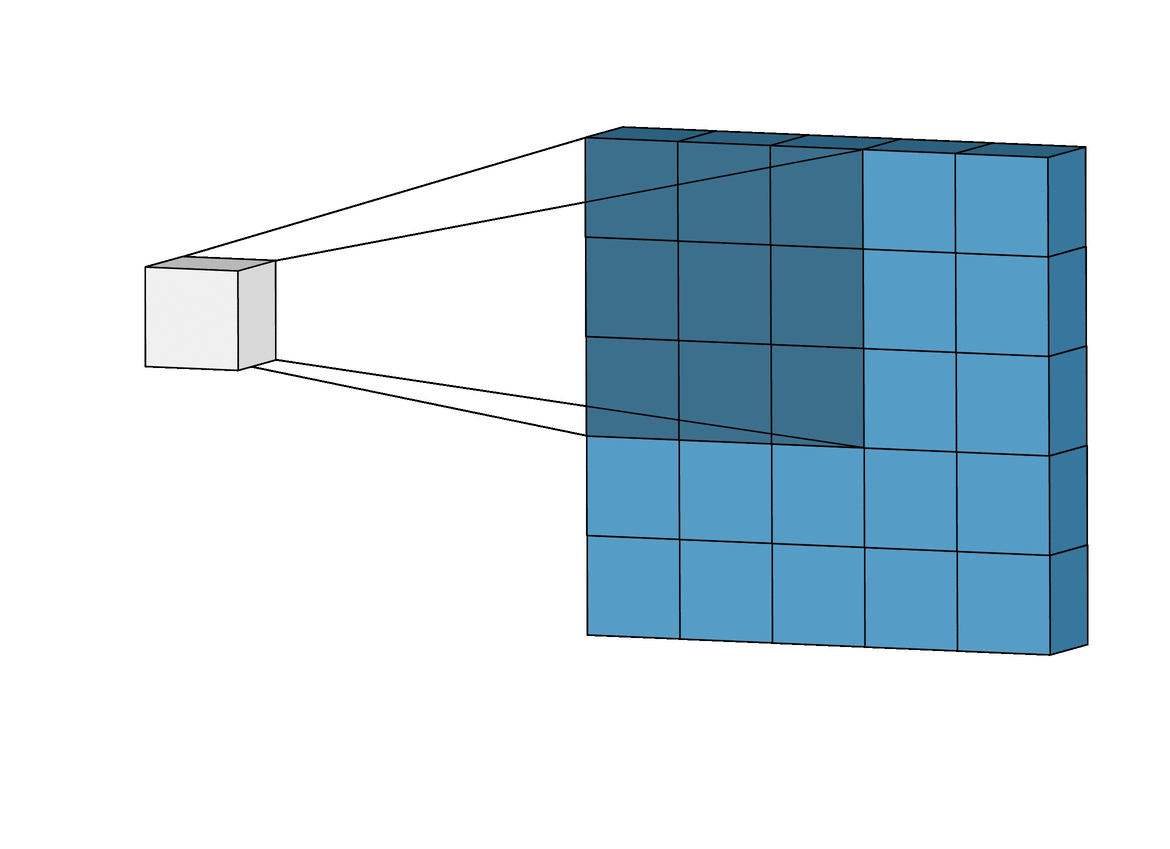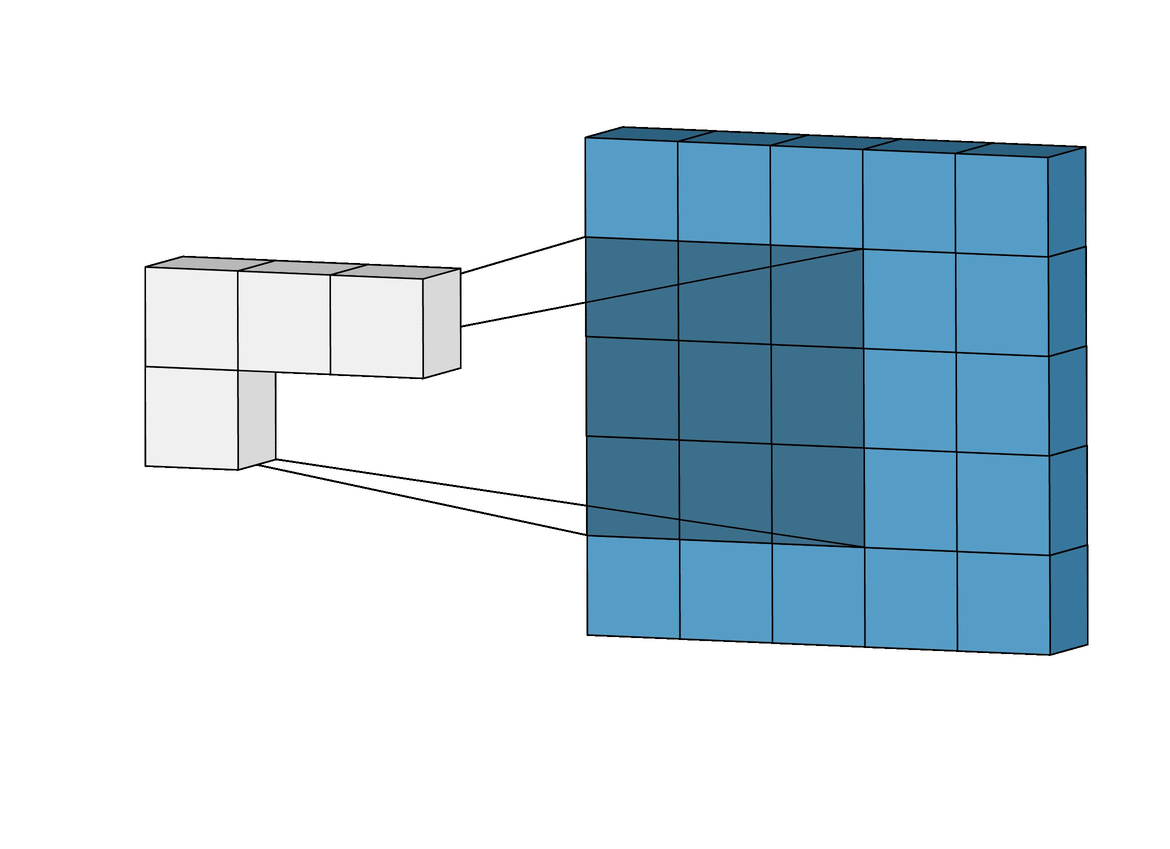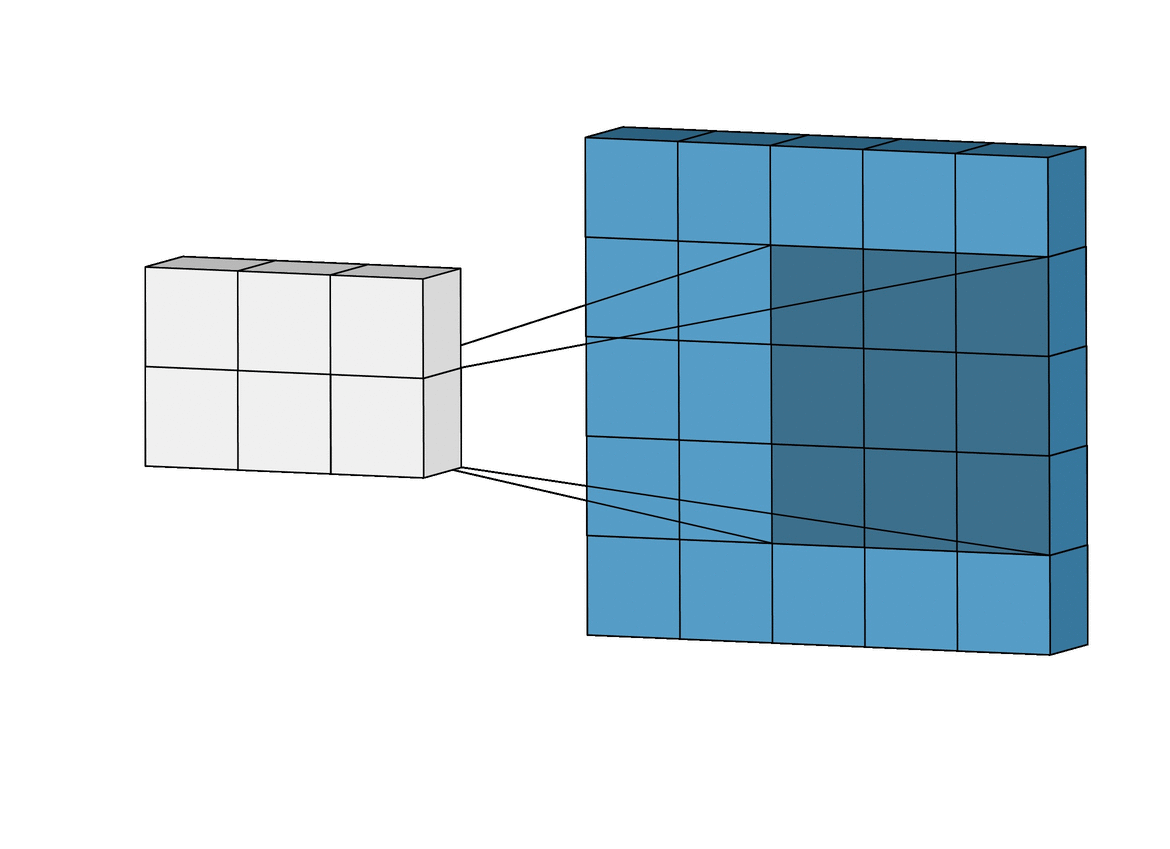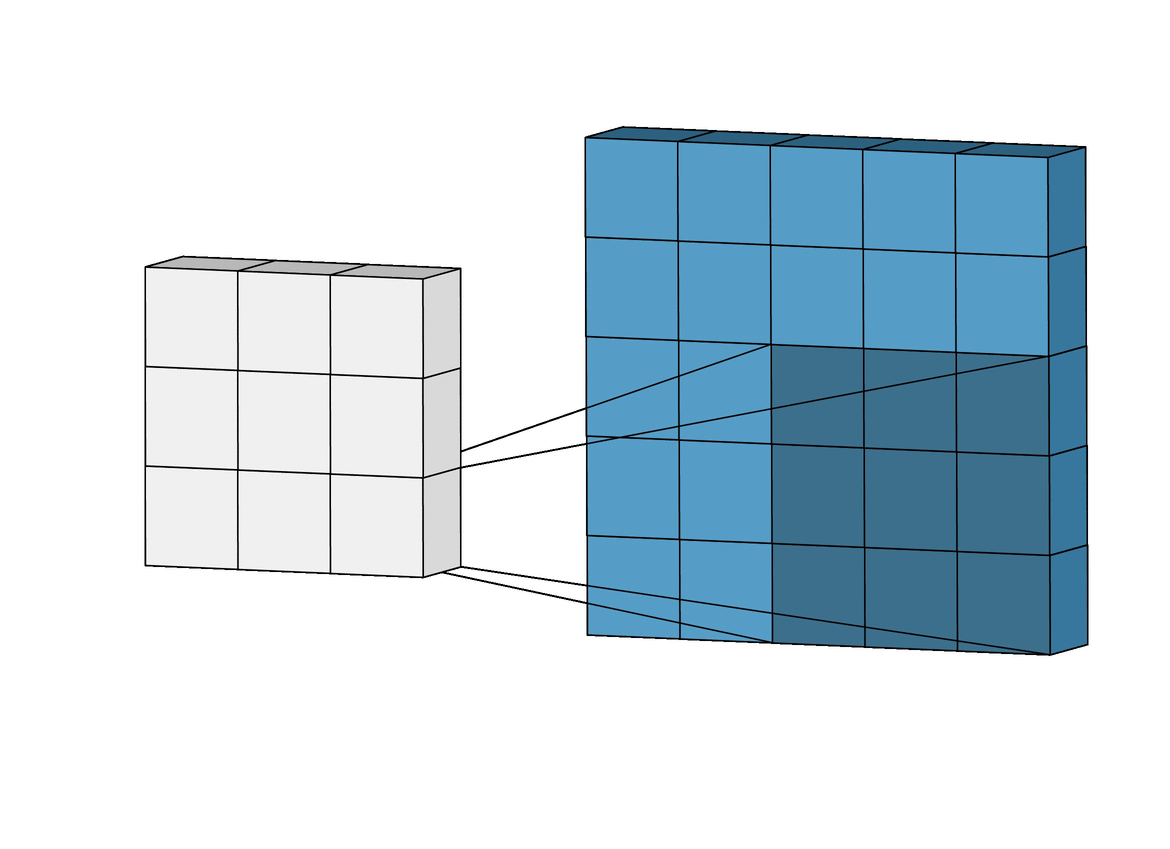
이 gif 그림을 통해 보면 더 CNN이 어떻게 Convolution 연산을 이용해서 시각 피질과 같은 결과를 내는지 한눈에 알아볼 수 있습니다. 더 자세한 것은 뒤에서 설명하도록 하겠습니다. (시각 피질의 Receptive field 아이디어)
파란색 직육면체 : Input image
흰색 직육면체 : Output (Feature map)
그림자 : 커널
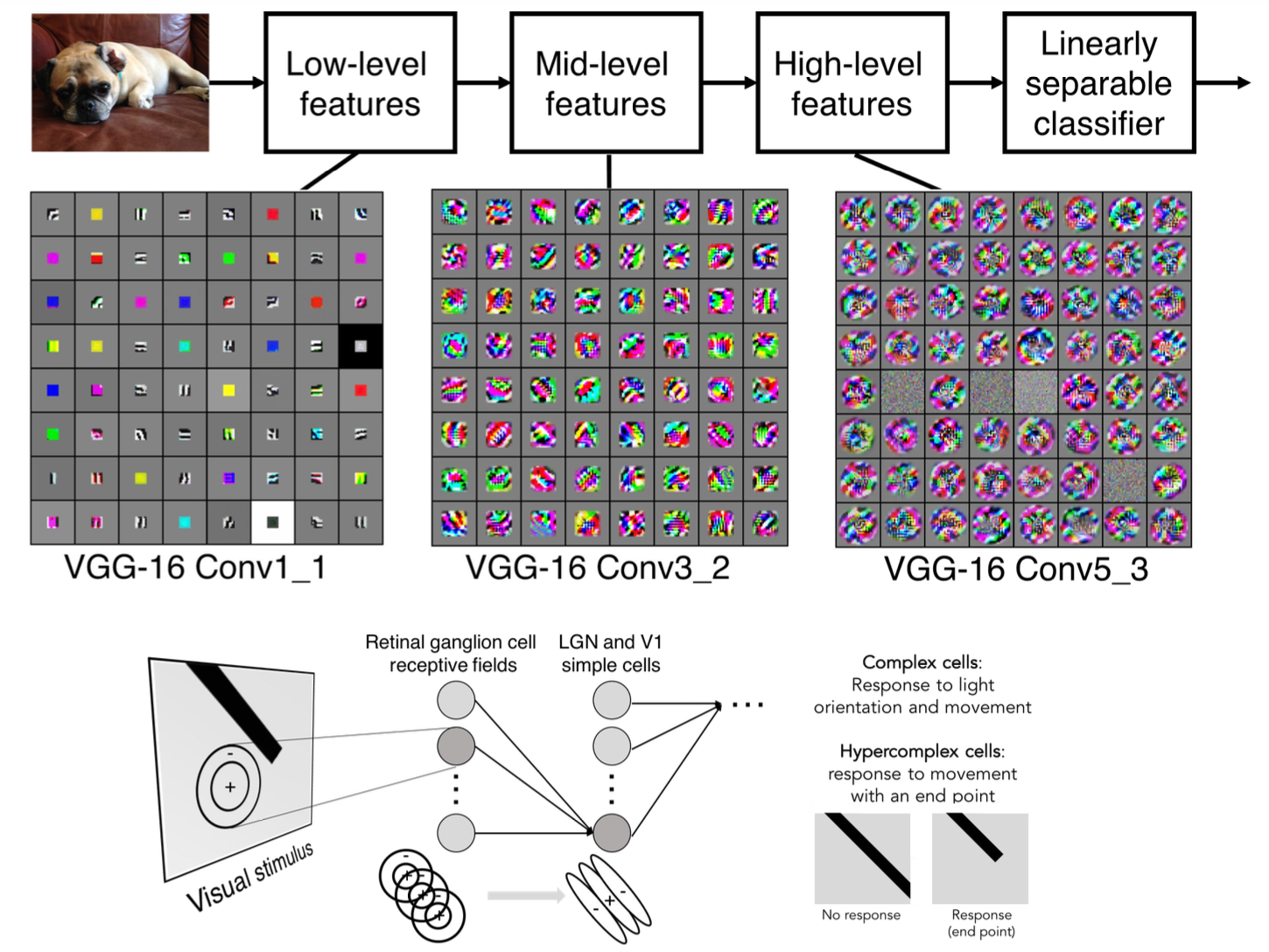
시각 피질은 또한 계층적 구조를 가진다고 이야기했었습니다. 위 그림에서는 시각 피질의 계층 구조를 CNN에 적용한 것을 볼 수 있는데요. VGG-16 모델의 중간 Feature map을 시각화한 모습입니다. VGG-16 모델은 간단히 말하면 Convolution layer를 여러 층으로 쌓아 구현한 모델입니다. 이것의 중간 Feature map을 통해 왼쪽과 같이 처음의 결과는 저수준의 특징을 잡아내지만 오른쪽으로 갈수록 고수준의 특징을 인식해 나가는 것을 볼 수 있습니다.
사실 저도 이게 어떤 것을 의미하는지 완벽히 이해하기는 어렵습니다만, 제가 이해한 바로는 저수준 특징은 사람이 쉽게 알아볼 수 있을 정도로 윤곽에 대한 정보만을 잡아내었고, 고수준은 사람이 이해하진 못하지만 컴퓨터가 자기만의 방식대로 특징들을 세세하게 잡아내었다고 생각하고 있습니다. 또한 이것과 함께 아까 뉴런의 계층적 인식 과정을 생각해 보았습니다. 저수준에서는 빛의 방향을 이해한다고 나왔었습니다. 이것을 봤을 때 빛이 들어오는 방향에 따라 윤곽을 이해하는 것이고, 고수준에서는 엣지를 이해한다고 했습니다. 이에 사람의 눈에는 명확하게 캐치되지 않는 엣지들까지 컴퓨터가 특징을 잡아내어 구분한다고 생각하면 되지 않을까 하는 직감을 가지고 있습니다. 하하
CNN 특징은 다음과 같은 것들이 있는데 추후 업데이트.. 예정..
1. Locality
2. Shared weights
4. CNN (Convolution Neural Network)
CNN (convolution neural network)은 여러 구조의 레이어들로 구성되어 있습니다.
이번 장에서는 이러한 CNN의 구조를 자세히 살펴보도록 하겠습니다.
4.1 Fully Connected Layer
지난 과정을 통해서 우리가 배운 네트워크들은 Fully Connected Layer를 활용하여서 학습을 진행했습니다.
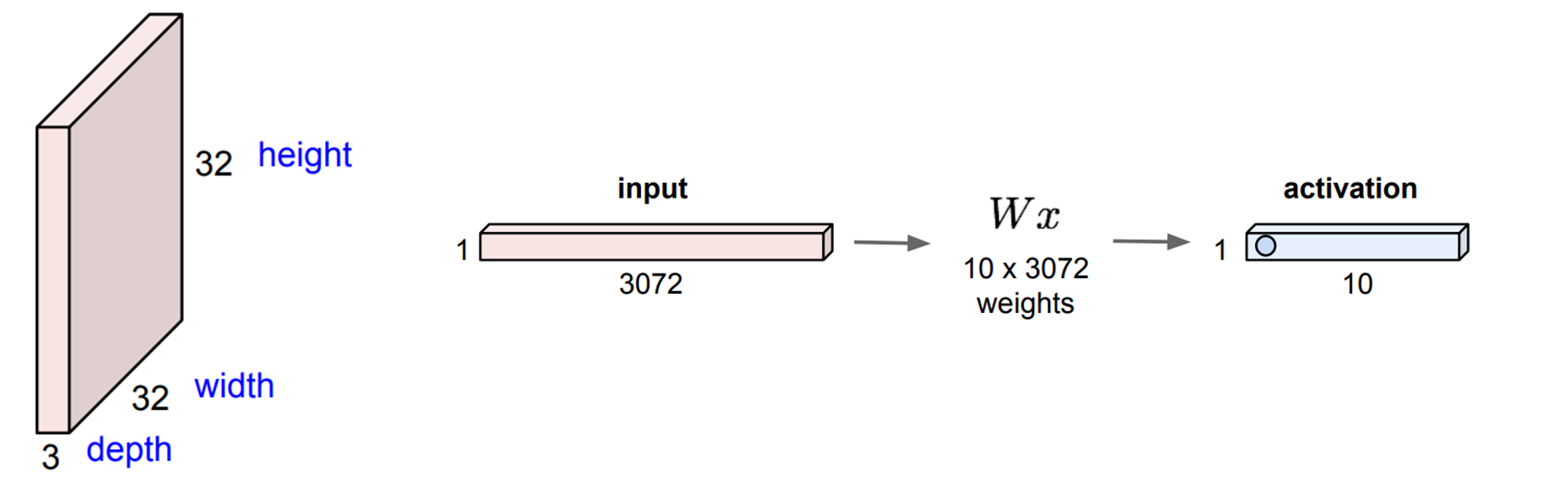
Fully Connected Layer를 활용해서 이미지를 학습한다고 한다면 위의 사진과 같은 과정으로 진행되어집니다.
먼저 우리에게 32 x 32 x 3 사이즈의 이미지 input data가 존재한다고 가정해 봅시다.
Fully Connected Layer 이러한 이미지를 학습하기 위해서 input의 형태를 변환시켜야 합니다.
즉, flatten 하여 1 x 3072의 형태로 input의 모습을 바꿔 주어야 합니다.
(여기서 3072는 32 x 32 x 3입니다)
그리고 우리가 생성한 가중치 W가 10 x 3072가 있다고 한다면 Fully Connected Layer에서 연산되어 나오는
Output은 1 x 10의 activation일 것입니다.
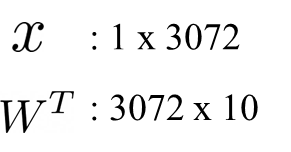
즉, 우리의 input을 x로 가정하고 W와 내적곱을 하게 된다면 (W의 row와 내적을 하기 때문에 전치해주어야 합니다)
1 x 10의 activation이 출력되게 되는 것입니다.
Fully Connected Layer는 연산량이 많아지고, 이미지 데이터의 Local 정보를 잃게 된다는 치명적인 단점이 있습니다.
오늘 배울 Convolutional Layer는 이러한 단점을 보완해 주는 Layer라고 할 수 있습니다.
4.2 Convolutional Layer
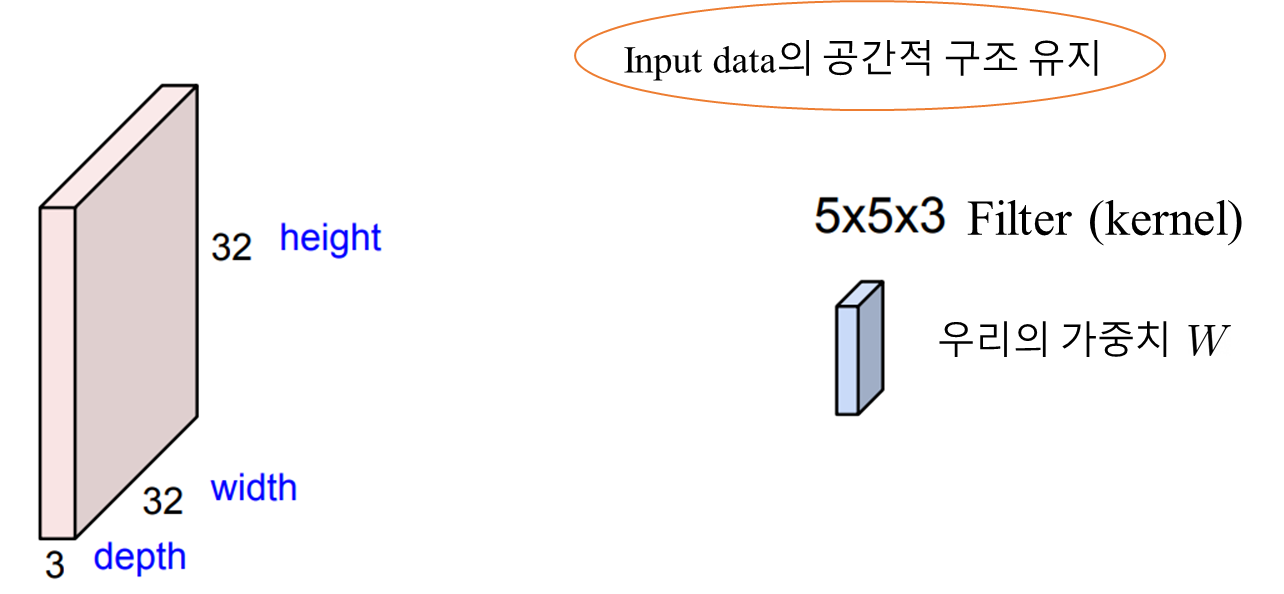
Convolutional Layer가 Fully Connected Layer와 확실한 차이점은 Input의 형태를 유지한 채 연산이 진행된다는 것입니다.
옆에와 같은 예시로 32 x 32 x 3 사이즈의 input data (image)가 존재한다고 했을 때 Convolutional Layer는 input의 형태를 그대로 보존하고 Filter를 활용해서 부분적으로 연산을 진행합니다.
여기서 필터의 사이즈인 5x5는 사용자가 Tensorflow나 Pytorch와 같은 프레임워크를 활용할 때 하이퍼 파라미터로 설정해 줄 수 있습니다.
그러면 여기서 의문이 하나 생길 수 있는데 이러한 필터(kernel)의 사이즈를
결정하는 방법이 무엇인지 궁금할 수가 있습니다.
물론 가장 먼저 사용자의 주관이 가장 큰 부분을 차지하지만,
GoogleNet과 같은 논문에 나오듯이 3x3 형태의 필터가 가장 좋은 성능을 보여준다는 연구결과가 있습니다.
(너무 작은 필터는 많은 연산을 일으키고, 너무 큰 필터는 공간 정보를 대략적으로 받아들이는 경향이 있습니다)
따라서 일반적으로는 3x3 형태의 필터사이즈를 사용하는 것이 성능을 향상시키기에 좋을 것입니다!
따라서 이렇게 만들어진 필터가 input 이미지를 stride 만큼 이동하면서 해당 부분과 필터의 내적곱을 진행하다고 이해하면 됩니다.
사실상 Fully Connected Layer의 가중치와 Convolutional Layer 필터가 같은 역할을 하는 것입니다!!
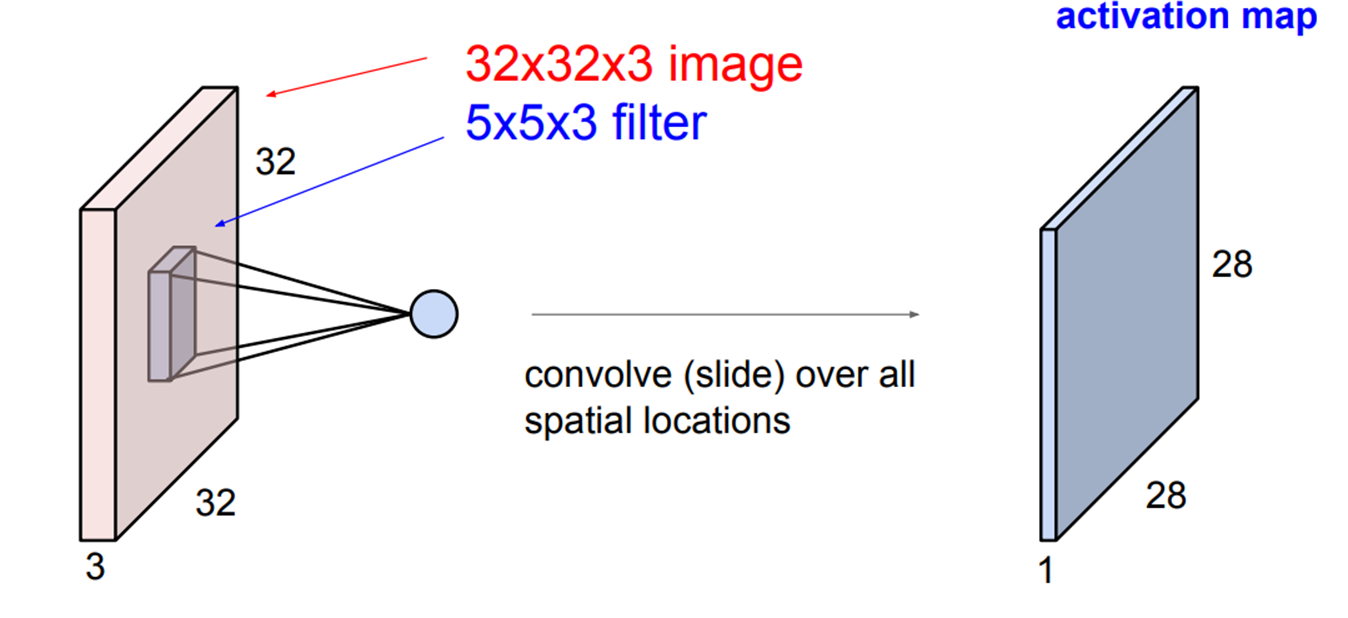
결국 이러한 과정을 통해서 32x32x3의 인풋 데이터가 들어갔을 때
filter의 사이즈가 5x5x3이라면 28x28x1 형태의 아웃풋이 만들어집니다.
여기서 input data의 차원이 3인데 왜 아웃풋의 차원은 1인가 하는 의문이 들 수 있습니다.
이를 예시로 자세히 설명해 보겠습니다.
여기서 인풋의 3차원은 RGB 값으로 3개의 차원을 갖습니다.
그리고 Filter의 차원도 인풋의 차원과 같게 설정을 해줍니다.
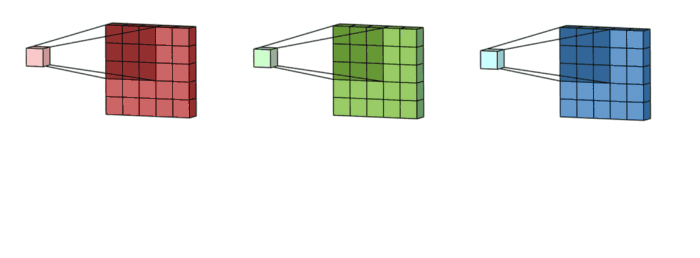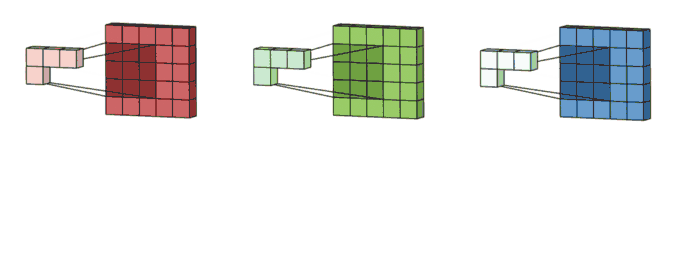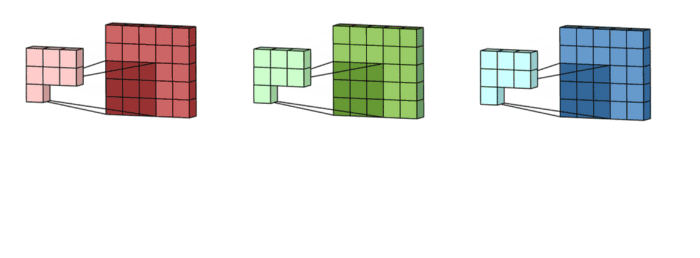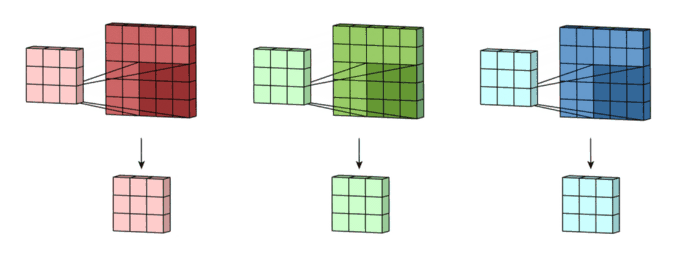
그런 다음 각 차원과 필터의 차원이 1:1대로 대응이 되어서 내적곱을 계산합니다. (이때 각 필터가 갖는 가중치는 같습니다)
그렇게 되면 (input : 5x5x3, filter : 3x3x3) 그렇게 되면 3x3 형태의 아웃풋이 3개가 형성되게 될 것입니다.
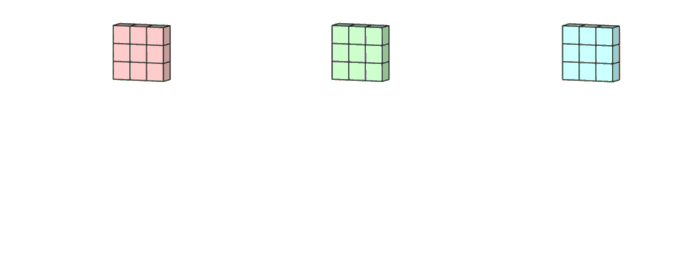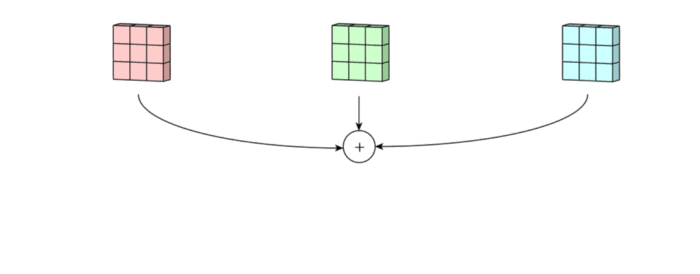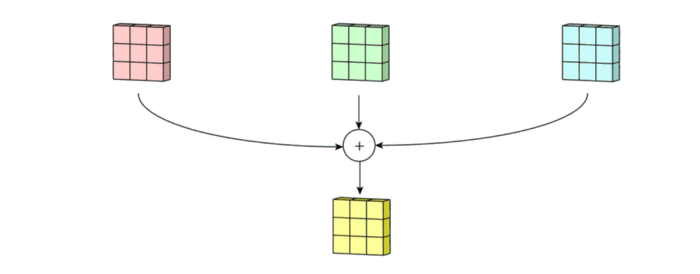
그런 다음 3개의 아웃풋을 합해주고 하나의 3x3x1 아웃풋을 만들어줍니다.
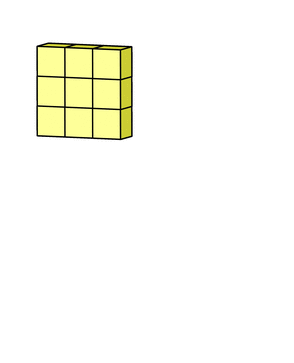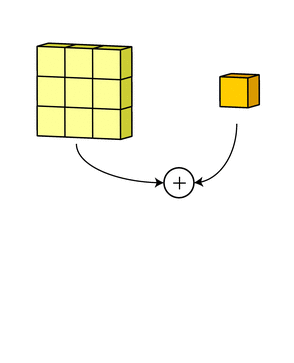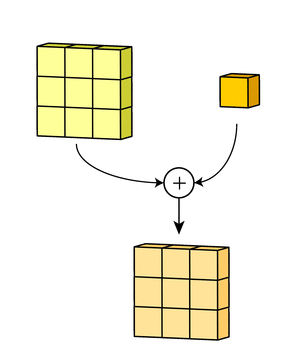
그리고 bias를 더해주어서 최종 아웃풋인 3x3x1 형태의 아웃풋이 형성되는 것입니다.
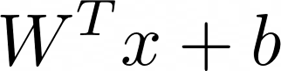
즉, 위의 수식을 시각화하여 Convolution 연산을 진행하게 되면 3x3x1 형태의 아웃풋이 만들어집니다.
따라서 아웃풋의 차원을 결정하는 것은 filter의 개수입니다.
만약 3x3x3 필터가 convoltional layer에 2개라면 아웃풋은 3x3x2가 만들어지고
6개라면 3x3x6의 아웃풋이 만들어집니다.
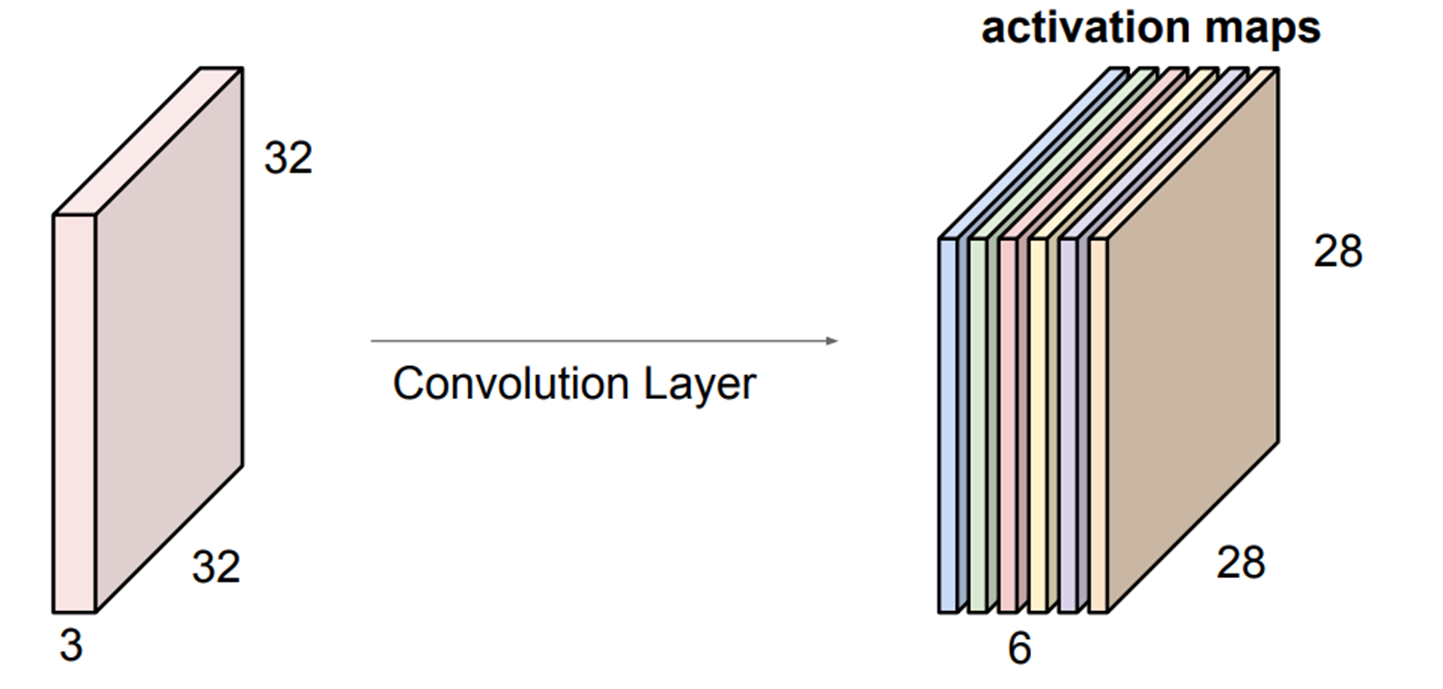
앞에서 나타는 32x32x3 input과 5x5x3 filter의 예시에 적용하게 되면
filter가 1개라면 28x28x1
filter가 2개라면 28x28x2
filter가 3개라면 28x28x3
의 결과값으로 나타나게 됩니다.
그러면 여기서 28x28의 output 사이즈는 어떻게 구해지는지 의문이 생길 수 있습니다.
이 부분은 Output Size에서 조금 더 상세히 살펴보겠습니다.
4.3 Output Size
먼저 7 x 7 형태의 인풋 이미지가 있고
우리가 3 x 3 형태의 filter를 활용해서 Convolution 연산을 진행해 본다고 가정해 보겠습니다.
여기서 Output Size에 영향을 주는 것에는
아래의 4가지가 있습니다
1. Input Size
2. Filter Size
3. Stride
4. Padding
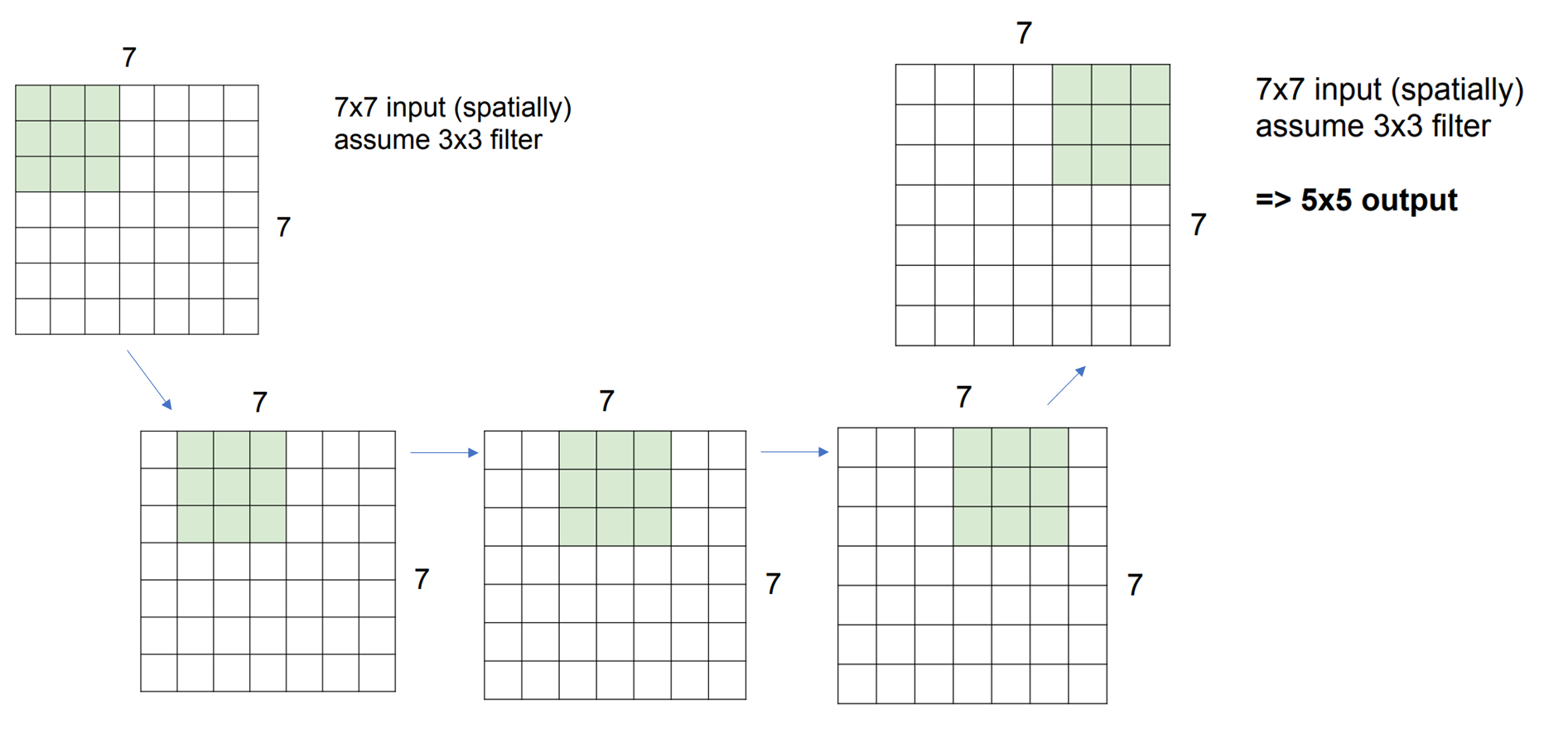
먼저 1~3번이 고려되는 상황을 살펴보겠습니다.
만약 위의 가정과 Stride가 1이라면 위의 과정으로 Convoltion 연산이 진행되게 됩니다.
즉, 한 칸씩 이동하면서 내적곱이 되는 것입니다.
이렇게 되면 행이 5이고 열이 5인 Output이 만들어집니다.
만약 Stried가 2라면 어떻게 될까요?
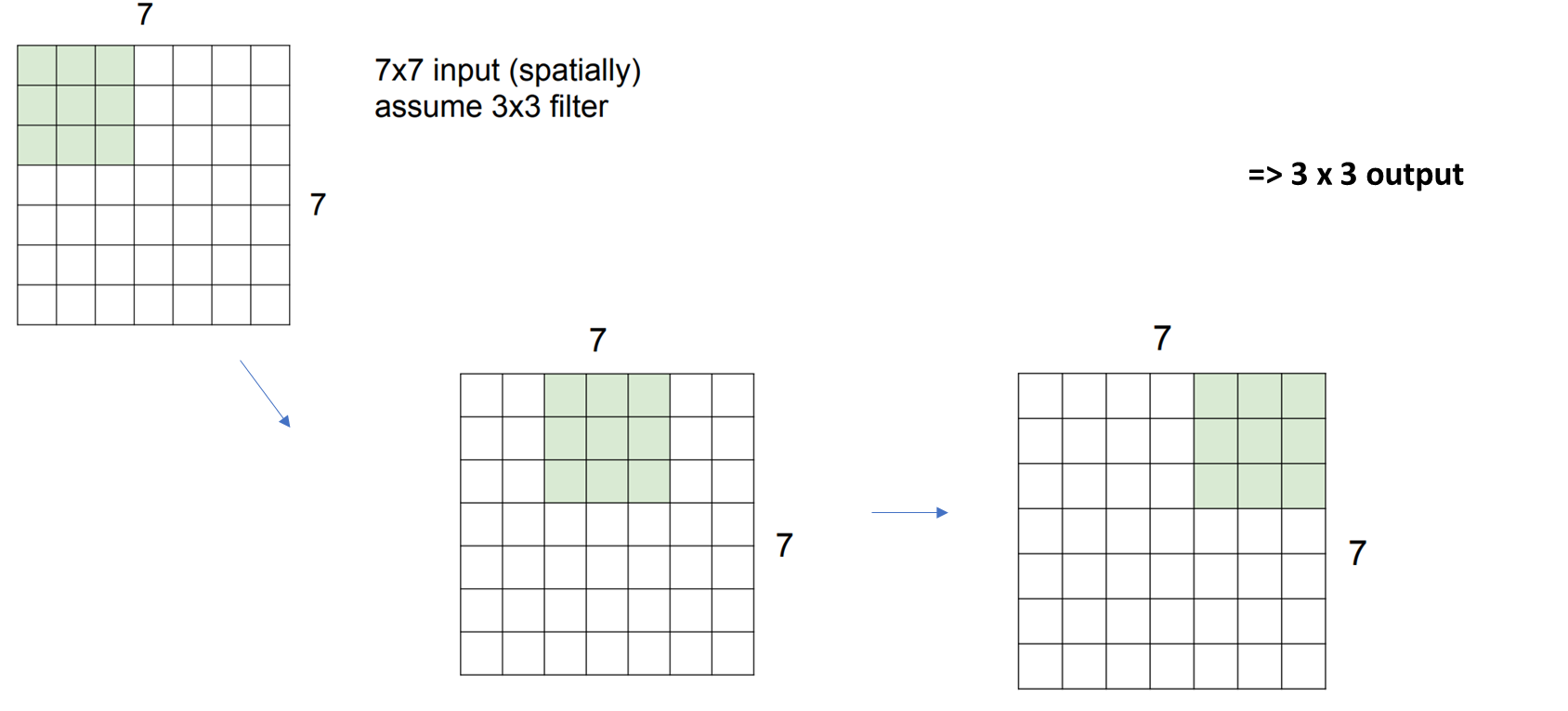
이번에는 2칸씩 이동하면서 필터와 부분값들이 내적곱이 되니까
3x3 형태의 아웃풋이 만들어지게 되는 것입니다
그렇다면 Stride가 3인 경우는요?
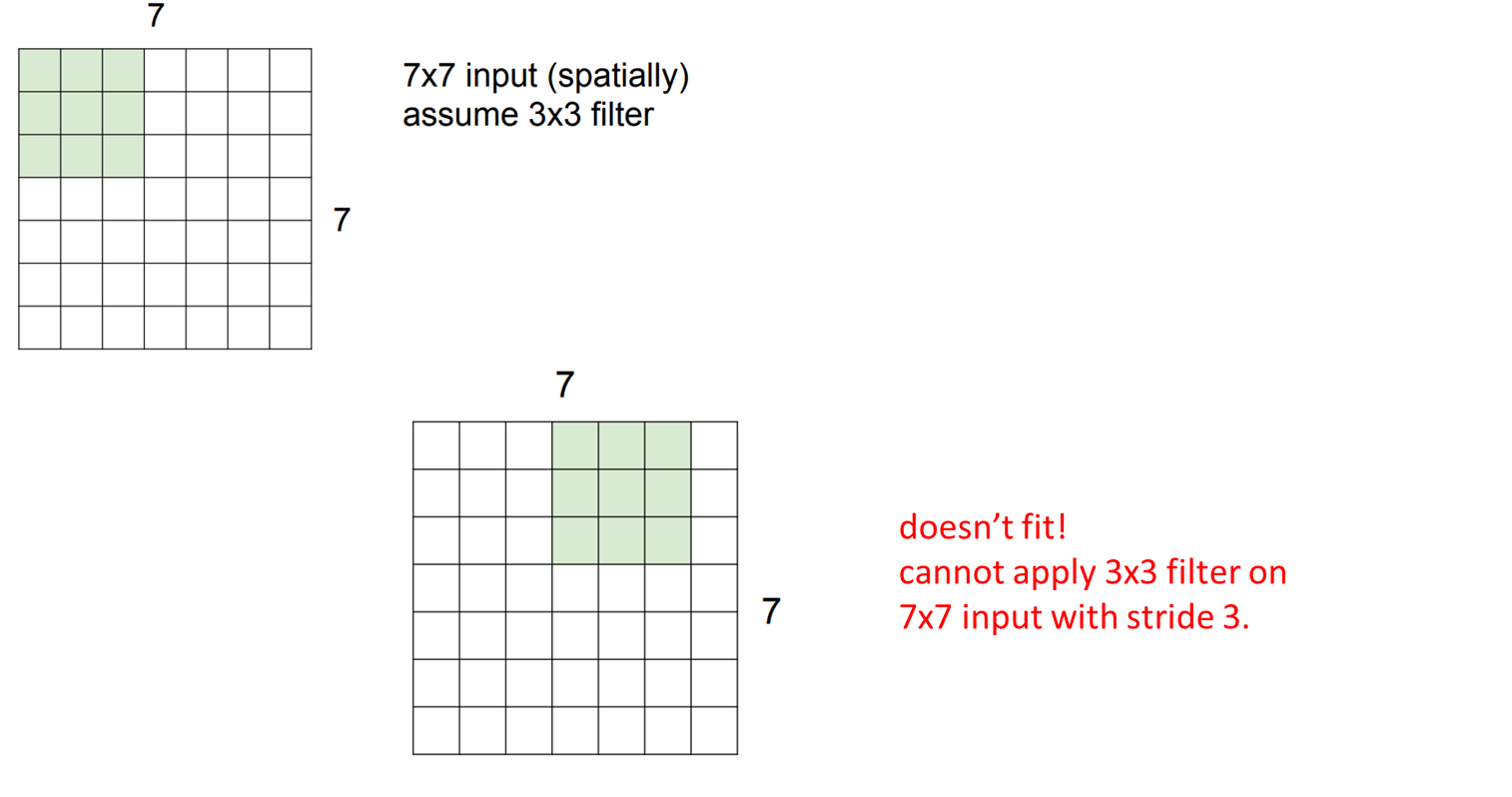
사진에서 볼 수 있듯이 연상이 진행되면서 마지막 column이 연산이 되지 않는 것을 확인할 수 있습니다.
즉, 위 상황에서 Stride가 3인 경우 제대로 연산이 진행되지 않습니다.
이렇게 Output Size가 결정되는 방식을 공식으로 정리하면 다음과 같습니다.
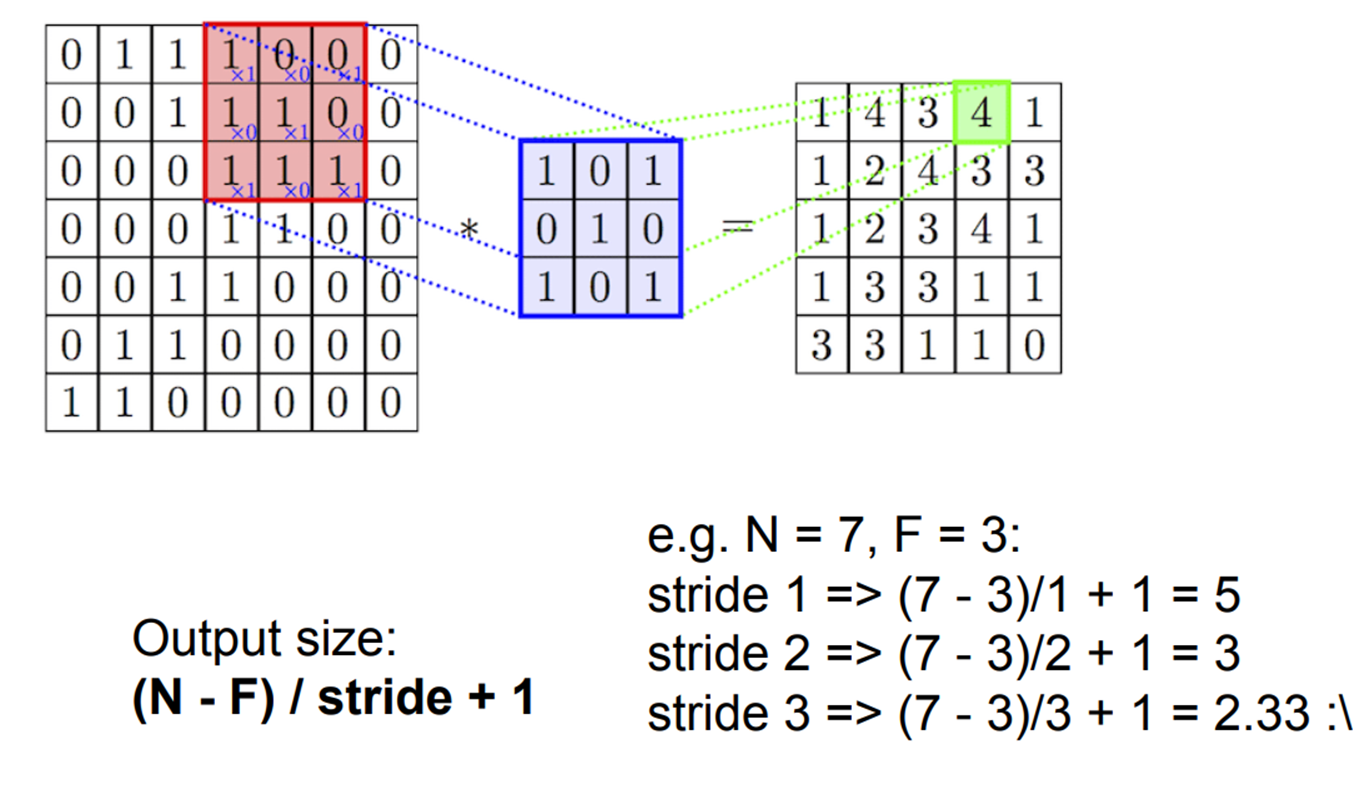
N은 Input data의 행 또는 열
F는 Filter의 행 또는 열입니다.
즉, 행이라고 가정한다면 input data의 행에서 Filter의 행을 빼주고 이를 stride 만큼 나누어준다음 1을 더해주면
Output의 행이 나오게 됩니다. (대부분 input data와 Filter의 Size는 행과 열을 같게 설정해 줍니다)
그렇게 되면 옆에 식들과 같이 정리할 수 있는데요
앞의 가정인 7x7 input과 3x3 필터를 활용하여 Stride의 값만을 변화했을 때 나오는 output들의 값들입니다.
여기서 눈에 띄는 것은 Output size의 결과가 정수로 나오지 않는다면 제대로 된 연산이 진행되지 않는다는 것을 알 수 있는데
이를 활용해서 사용자가 하이퍼 파라미터로 Stride를 결정할 수 있는 방법으로 활용할 수 있습니다.
여기서 Stride의 수의 차이가 어떠한 결과를 만드는지에 대한 의문이 생길 수 있습니다.
뒤에서 나오겠지만 Stride 수의 변화로 Pooling과 같은 downsampling의 효과를 얻을 수 있습니다.
Padding
그런데 여기서 Output Size를 결정하기 위해서 고려해야 할 하나가 더 있습니다.
앞으로 돌아가서 Convolution 연산 과정을 시각화한 이미지를 다시 한번 살펴봅시다.

뭔가 의문이 생기거나 이상한 부분이 없으신가요?
바로 corner 부분의 값들과 연산이 한 번씩 밖에 이루어지지 않는다는 것입니다.
즉, Corner 부분이 다른 값들과 비교했을 때 손실된다고 여겨질 수 있습니다.
이러한 부분을 해결하기 위해 활용되는 방법이 Padding입니다.
또한 Convolution 연산을 하게 되면 이미지의 사이즈가 줄어드는데 이를 방지하기 위해서 (즉, downsampling을 막기 위해서) 활용되기도 합니다
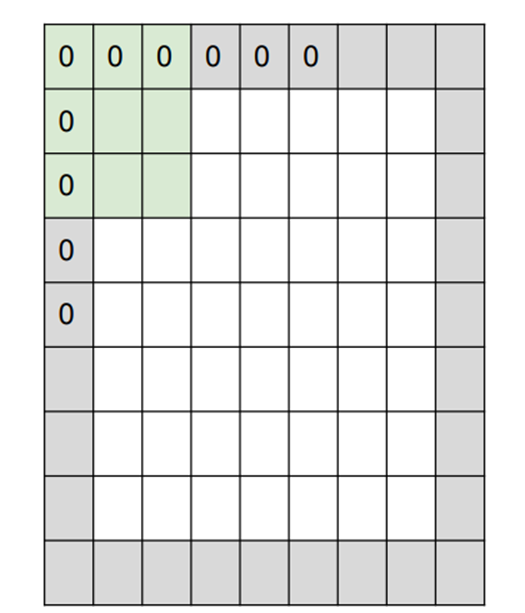
쉽게 말해서 원본데이터에 이렇게 0으로 한 겹 쌓아서 새로운 Input data를 만들어 내는 것입니다,
이런 경우 기존의 input data가 N x N이라고 한다면 padding : 1 추가했을 때
새롭게 만들어지는 input은 (N+2) x (N+2)이 되고 앞에서 배운 공식에 대입한다면
Output Size = (N + 2 - F) / stride + 1가 된다고 할 수 있습니다.
이를 공식으로 정리하면
(N – F + 2P) / Stride + 1이고
여기서 P는 padding의 수입니다.
4.4 Pooling
Convolution Layer 뿐만 아니라 CNN을 구성하는 레이어에는 Pooling Layer가 있습니다.
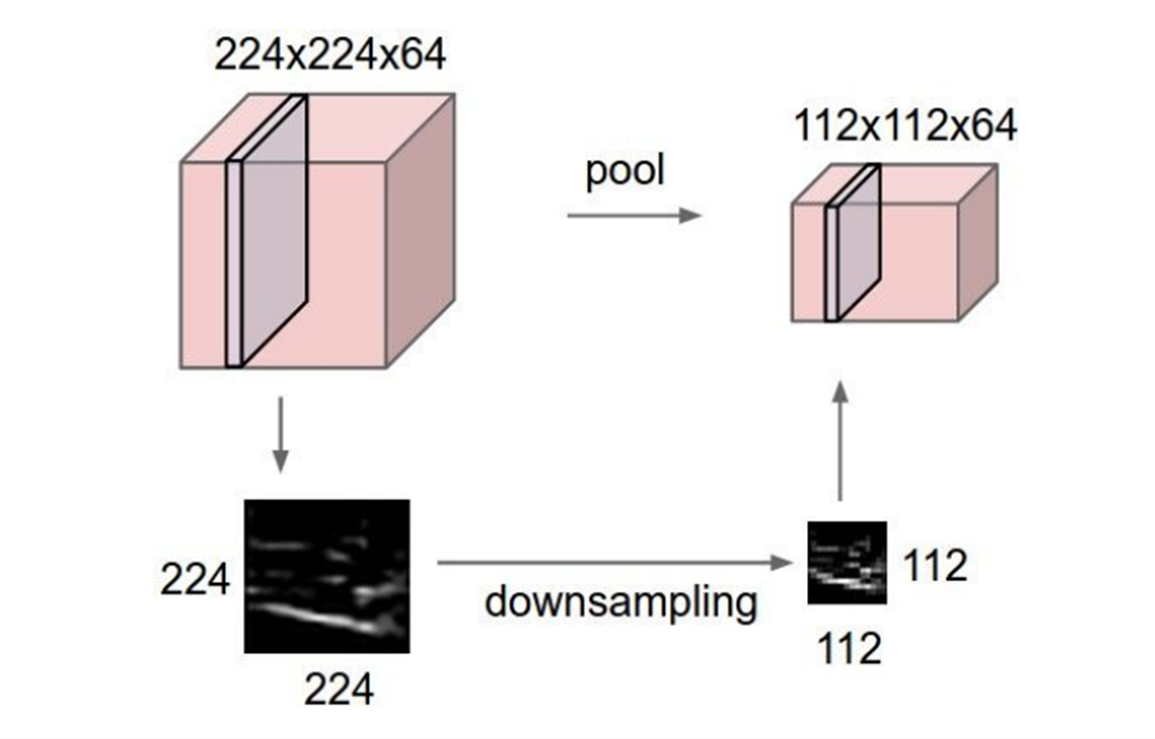
Pooling Layer의 목적은 downsampling입니다.
왜 downsampling이 필요할까요?
이는 깊은 모델을 학습하기 위해서입니다.
Vgg - 16과 같은 깊은 모델을 학습하게 되면 깊어질수록 파라미터의 개수가 증가합니다.
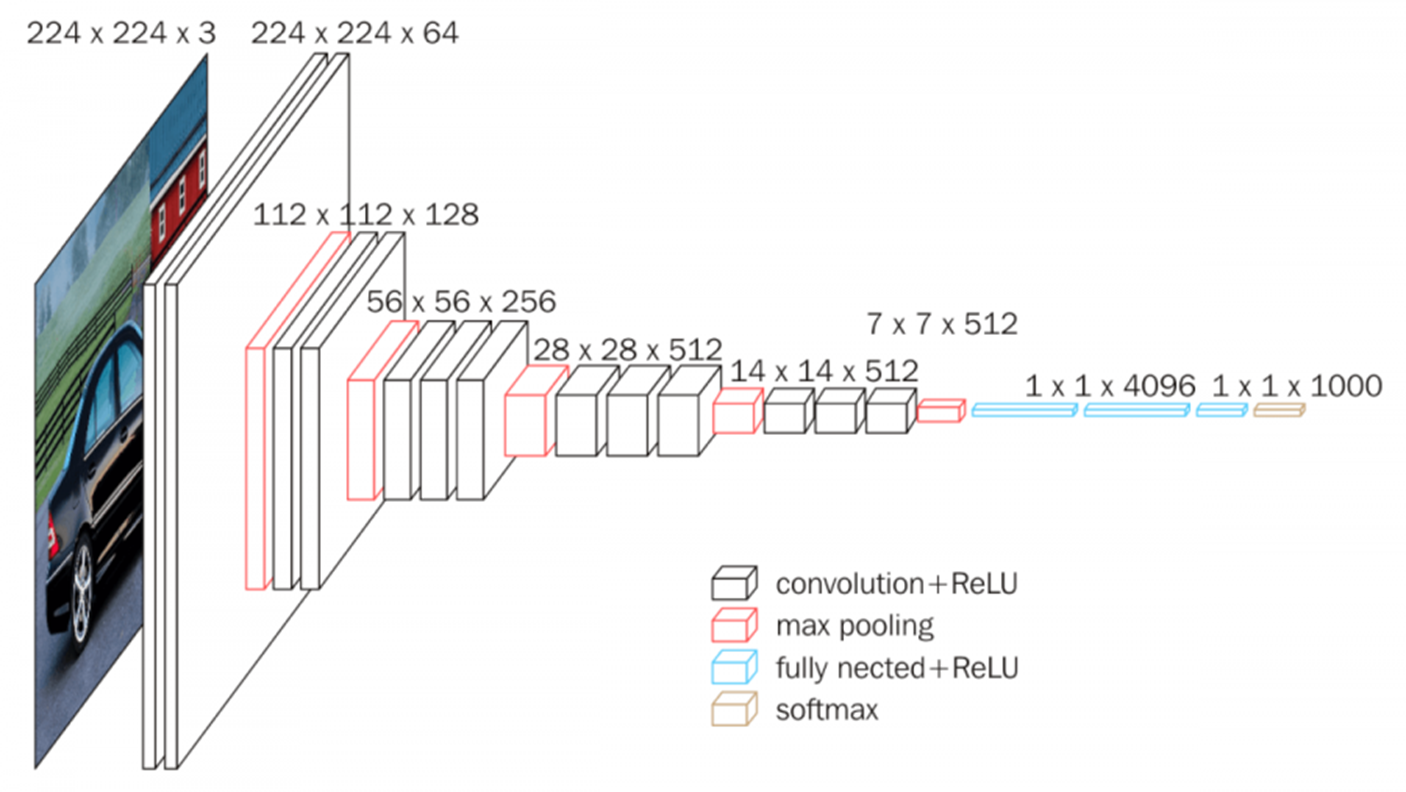
따라서 우리가 갖고 있는 하드웨어의 성능이 한계가 있기 때문에 이를 맞추기 위해서 downsampling을 필수적입니다.
이러한 목적을 위해서 Pooling Layer가 활용됩니다.
Pooling 방법에는 크게
Max pooling과 Average pooling이 있습니다.
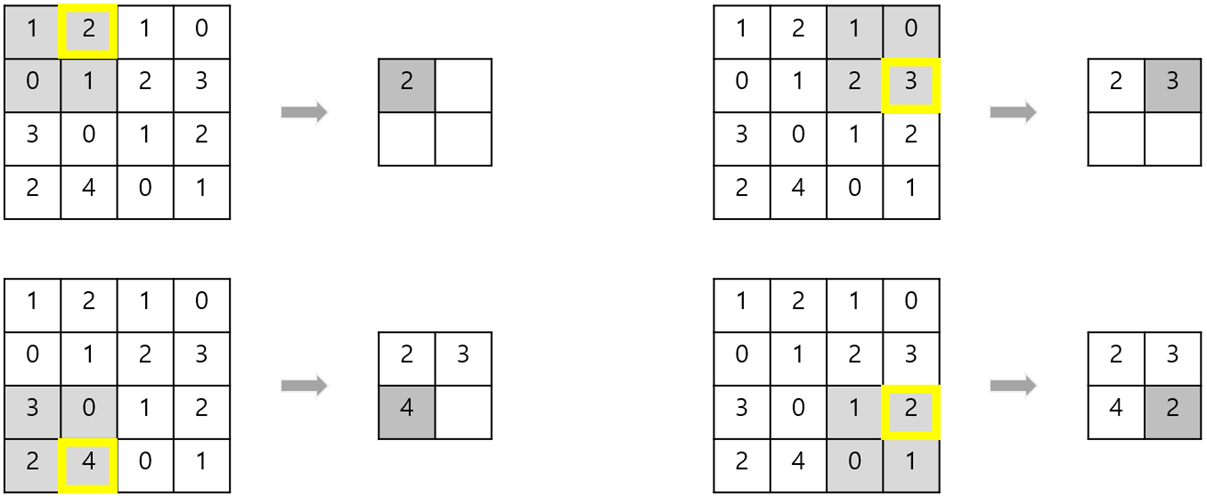
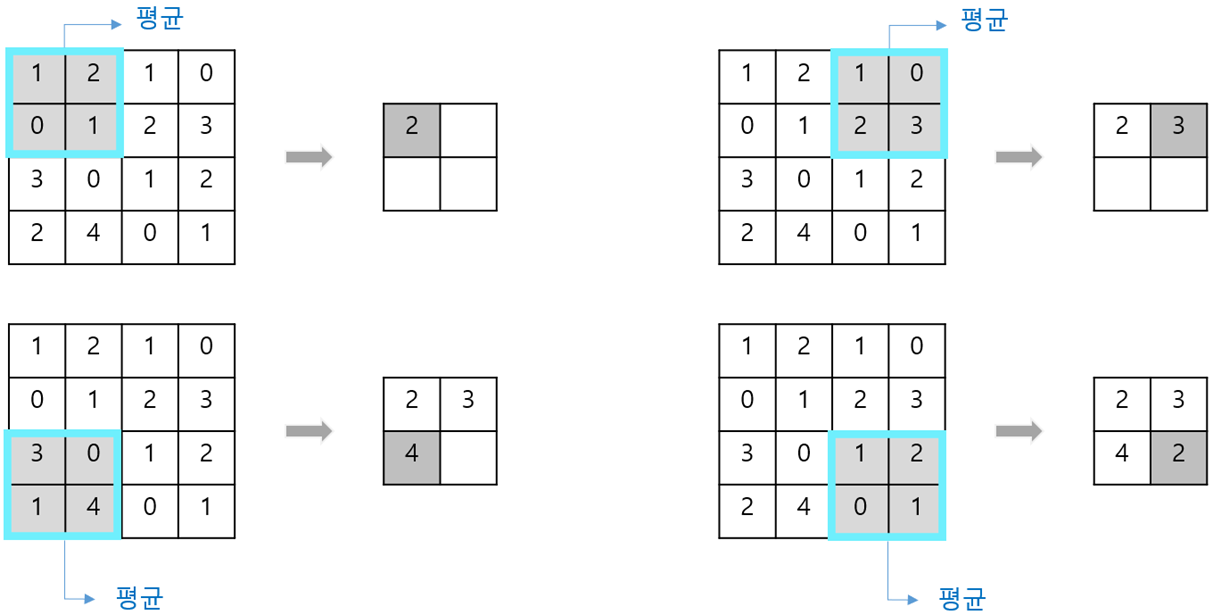
Max pooling의 경우 해당 부분의 최댓값을 대표값으로하고 Average Pooling의 경우 평균값을 대표값으로 해서
Output을 만들어 냅니다.
또한 Pooling의 경우 학습파라미터가 존재하지 않습니다!
또한 Stride를 조정함으로써 Pooling의 효과인 Down sampling을 가져올 수 있는데
최근 연구에서는 이러한 Pooling 보다는 Stride를 조정해서 Downsampling 하는 방법이 선호되고 있습니다.
Summary
이렇게 Convolution Layer, Pooling Layer, 그리고 뒤에 배울 Batch Normalization과 같은 다양한 Layer와 저번 시간에 배운 비선형 함수가 차례대로 번갈아 가면서 구성되면서 만들어지는 네트워크를 CNN이라고 할 수 있습니다.
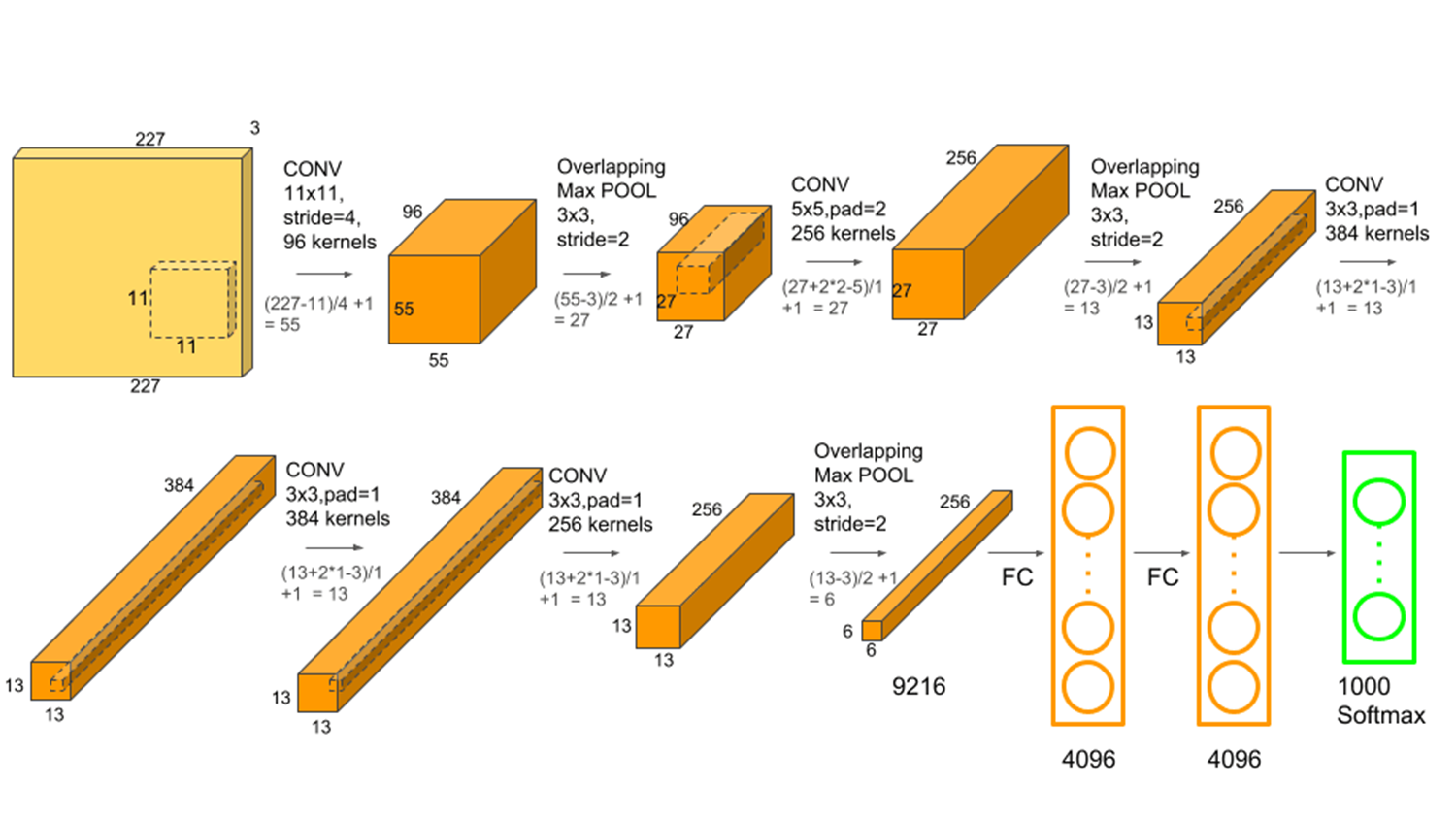
위 사진은 본격적으로 CNN의 시대를 연 AlexNet 모델의 구조입니다.
여기서에서 확인할 수 있듯이 Convolution Layer(padding, 비선형함수) , Pooling이 계속해서 연결되어 있는 것을 확인할 수 있고 마지막 부분에 도착했을 때 Fully Connected Layer의 연산과 Softmax를 통과해서 분류가 되는 것을 확인할 수 있습니다.
(여담으로 파라미터의 개수의 경우 FC 레이어에 도착했을 때 급격하게 증가하기 때문에, 최근에는 FC레이어를 제거하거나 줄이는 방향으로 연구가 진행되고 있습니다)

Kovi는 SSDC(Samsung Software Developer Community)를 기반으로 만들어진 커뮤니티입니다. ML, DL, Computer Vision, Robotics에 관심 있고 열정 있는 사람들이 모여 함께 활동 중입니다.
Kovi Instagram : https://www.instagram.com/kovi.or.kr/
Kovi SSDC : https://software.devcommunities.net/community/communityDetail/98
이 포스팅은 Kovi 커뮤니티 스터디의 일환으로 작성되었습니다.
posted by. Panda99 & Daevi
'CS231n' 카테고리의 다른 글
| [CS231n] Lecture 7. Training Neural Networks II (0) | 2023.03.04 |
|---|---|
| [CS231n] Lecture 6. Training Neural Networks 1 (수정 중) (0) | 2023.03.02 |
| [CS231n] Lecture 4. Backpropagation and Neural Networks (0) | 2023.02.14 |
| [CS231n] Lecture 3. Loss Functions and Optimization (0) | 2023.02.04 |
| [CS231n] Lecture 2. Image Classification (0) | 2023.02.03 |